Two_Proportions

The TeachBayes package has several functions to facilitate working with a discrete prior for two proportions.

library(TeachBayes)

Uniform Prior

Start with a uniform prior on (p1, p2), where each proportion takes on values .05, .15, …, .95.

prior <- testing_prior(.05, .95, 10,
                       uniform=TRUE)

Construct a graph of this distribution.

draw_two_p(prior)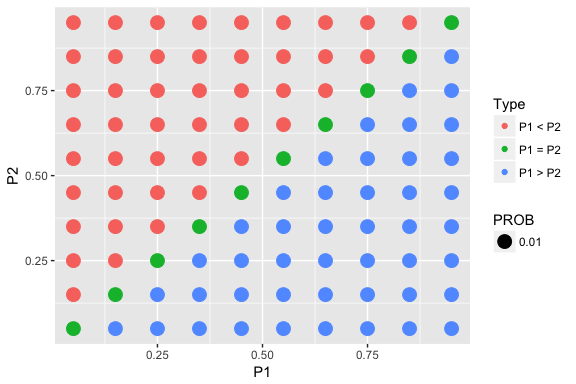

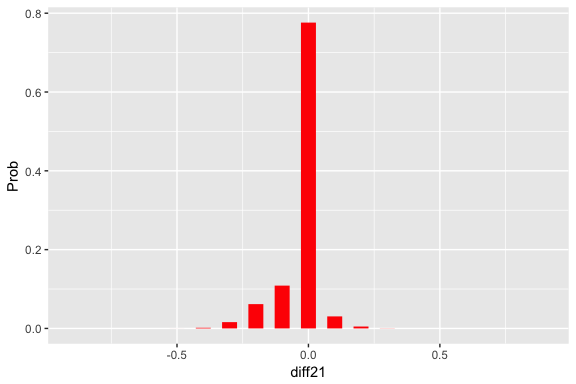
This finds the probability distribution of the difference in proportions p1 - p2, and plots the distribution.

(diff_dist <- two_p_summarize(prior))

## # A tibble: 19 x 2
##    diff21  Prob
##     <dbl> <dbl>
##  1   -0.9  0.01
##  2   -0.8  0.02
##  3   -0.7  0.03
##  4   -0.6  0.04
##  5   -0.5  0.05
##  6   -0.4  0.06
##  7   -0.3  0.07
##  8   -0.2  0.08
##  9   -0.1  0.09
## 10    0    0.1 
## 11    0.1  0.09
## 12    0.2  0.08
## 13    0.3  0.07
## 14    0.4  0.06
## 15    0.5  0.05
## 16    0.6  0.04
## 17    0.7  0.03
## 18    0.8  0.02
## 19    0.9  0.01

prob_plot(diff_dist)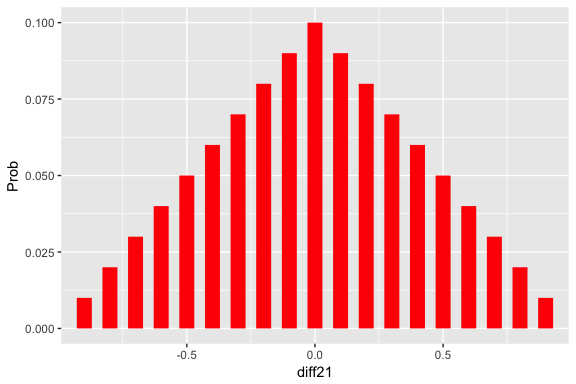

Collect some data from two binomial samples.

y1n1 <- c(10, 20)
y2n2 <- c(8, 24)

Update (find posterior):

post <- two_p_update(prior, y1n1, y2n2)

Graph and summarize:

draw_two_p(post)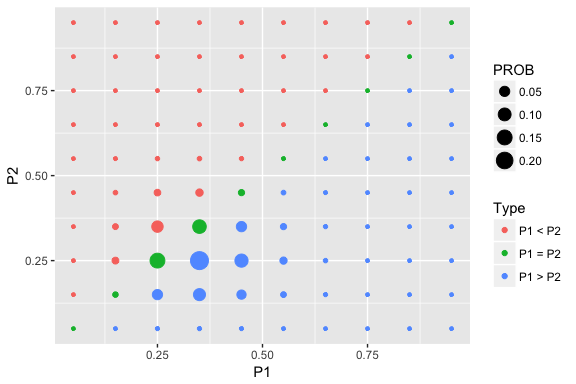

prob_plot(two_p_summarize(post))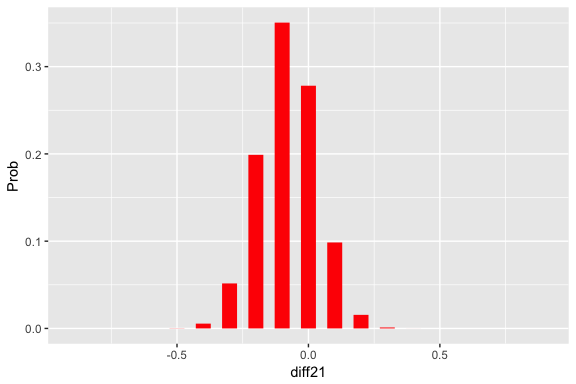

Testing Prior

prior <- testing_prior(.05, .95, 10, pequal=0.5)

Construct a graph of this distribution and summarize.

draw_two_p(prior)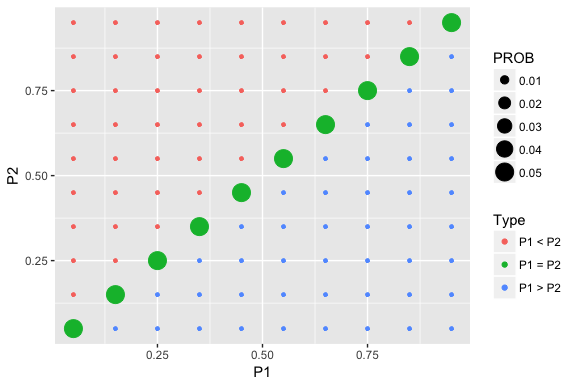

prob_plot(two_p_summarize(prior))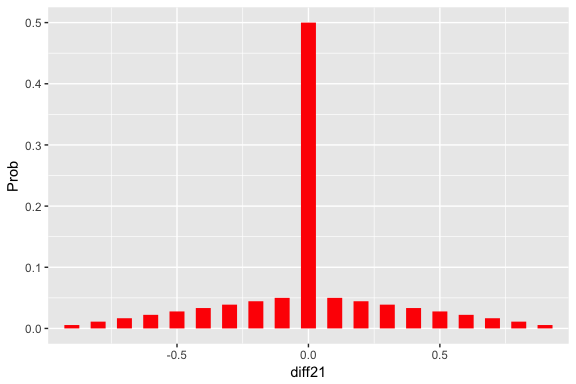

Collect some data from two binomial samples.

y1n1 <- c(10, 20)
y2n2 <- c(8, 24)

Update (find posterior):

post <- two_p_update(prior, y1n1, y2n2)

Graph and summarize:

draw_two_p(post)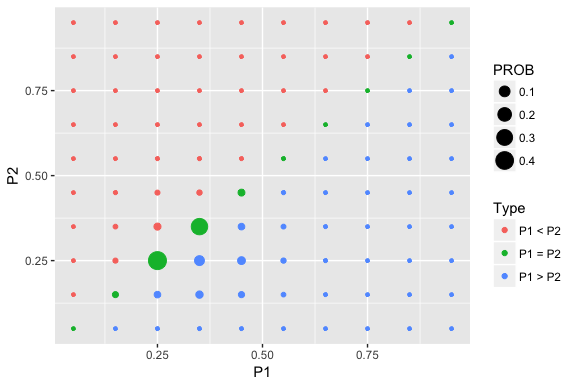

prob_plot(two_p_summarize(post))