Chapter 5 Introduction to Bayesian Computation

5.1 A Beta-Binomial Model for Overdispersion

library(LearnBayes)

First consider posterior of \((\eta, K)\).

mycontour(betabinexch0,
          c(.0001, .003, 1, 20000),
          cancermortality,
          xlab="eta", ylab="K")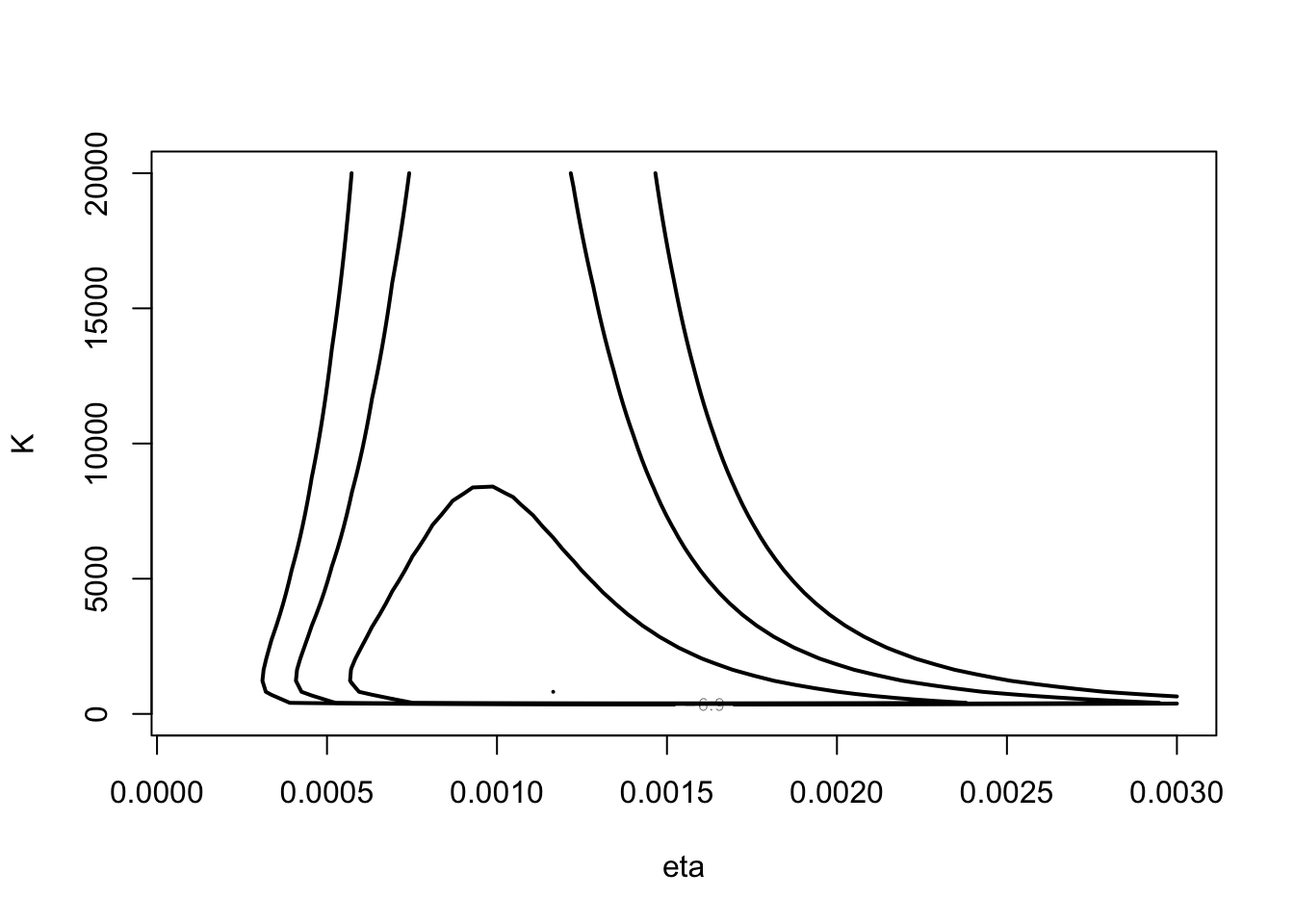

Instead look at posterior of \((\log \frac{\eta}{1-\eta}, \log I\).

mycontour(betabinexch,
          c(-8, -4.5, 3, 16.5),
          cancermortality,
          xlab="logit eta", ylab="log K")

5.2 Approximations Based on Posterior Modes

fit <- laplace(betabinexch, 
               c(-7, 6), 
               cancermortality)
fit

## $mode
## [1] -6.819793  7.576111
## 
## $var
##             [,1]       [,2]
## [1,]  0.07896568 -0.1485087
## [2,] -0.14850874  1.3483208
## 
## $int
## [1] -570.7743
## 
## $converge
## [1] TRUE

npar <- list(m=fit$mode, v=fit$var)
mycontour(lbinorm,
          c(-8, -4.5, 3, 16.5), 
          npar,
          xlab="logit eta", ylab="log K")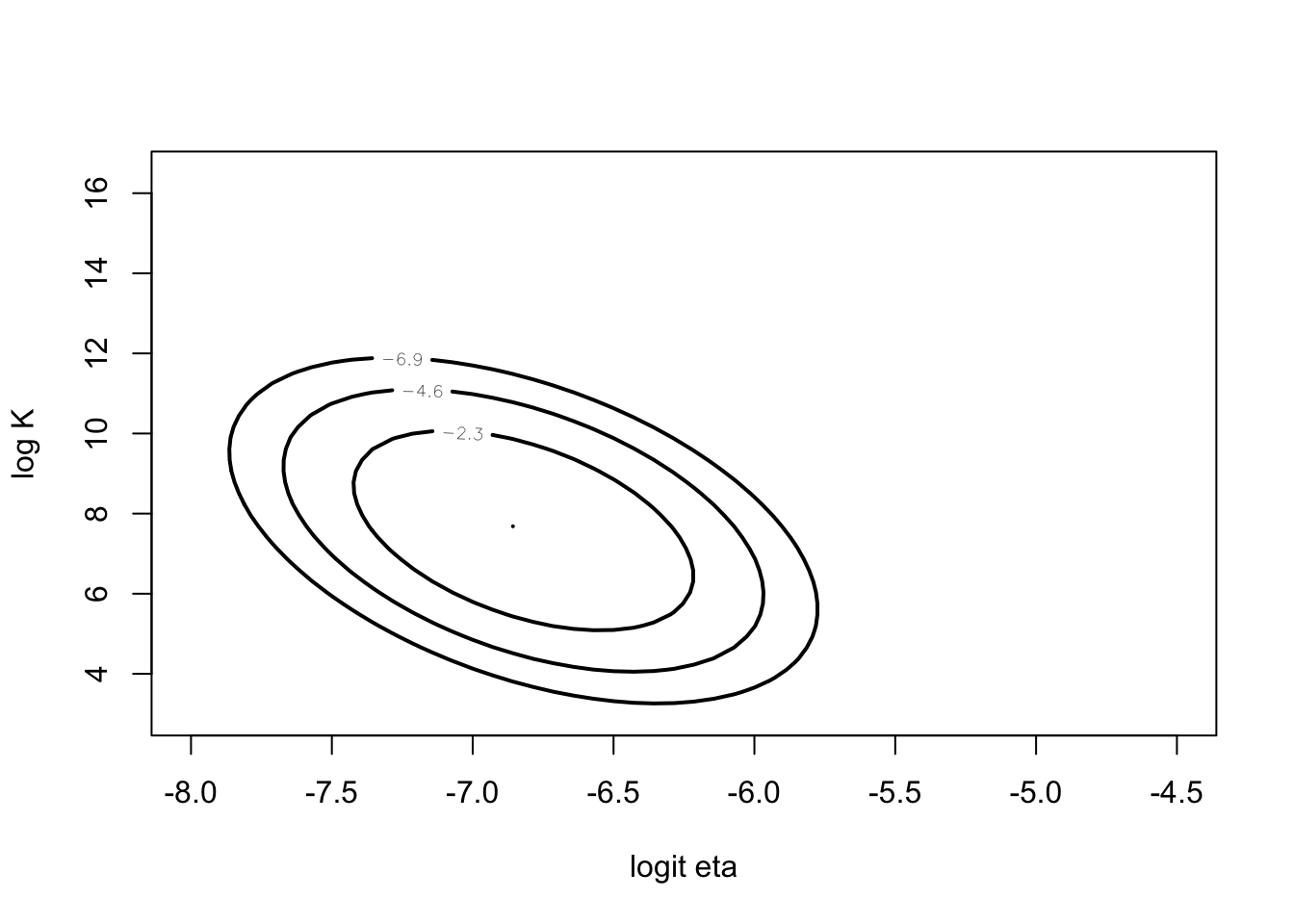

se <- sqrt(diag(fit$var))
fit$mode - 1.645 * se

## [1] -7.282052  5.665982

fit$mode + 1.645 * se

## [1] -6.357535  9.486239

5.3 Monte Carlo Method for Computing Integrals

Illustration of a simple estimate of an integral by Monte Carlo.

p <- rbeta(1000, 14.26, 23.19)
est <- mean(p ^ 2)
se <- sd(p ^ 2) / sqrt(1000)
c(est,se)

## [1] 0.150436813 0.001985356

5.4 Rejection Sampling

Using rejection sampling for the overdispersion posterior with a multivariate t proposal density.

fit <- laplace(betabinexch,
               c(-7, 6),
               cancermortality)

betabinT <- function(theta, datapar){
  data <- datapar$data
  tpar <-datapar$par
  d <- betabinexch(theta,data) -
         dmt(theta, mean=c(tpar$m),
             S=tpar$var, df=tpar$df, log=TRUE)
  d
}

tpar <- list(m=fit$mode, var=2 * fit$var, df=4)
datapar <- list(data=cancermortality, par=tpar)

start <- c(-6.9, 12.4)
fit1 <- laplace(betabinT, start, datapar)
fit1$mode

## [1] -6.888963 12.421993

betabinT(fit1$mode, datapar)

## [1] -569.2829

theta <- rejectsampling(betabinexch,
                        tpar,
                      -569.2813, 
                      10000,
                      cancermortality)
dim(theta)

## [1] 2438    2

mycontour(betabinexch, 
          c(-8, -4.5, 3, 16.5), 
          cancermortality,
          xlab="logit eta", ylab="log K")
points(theta[,1],theta[,2])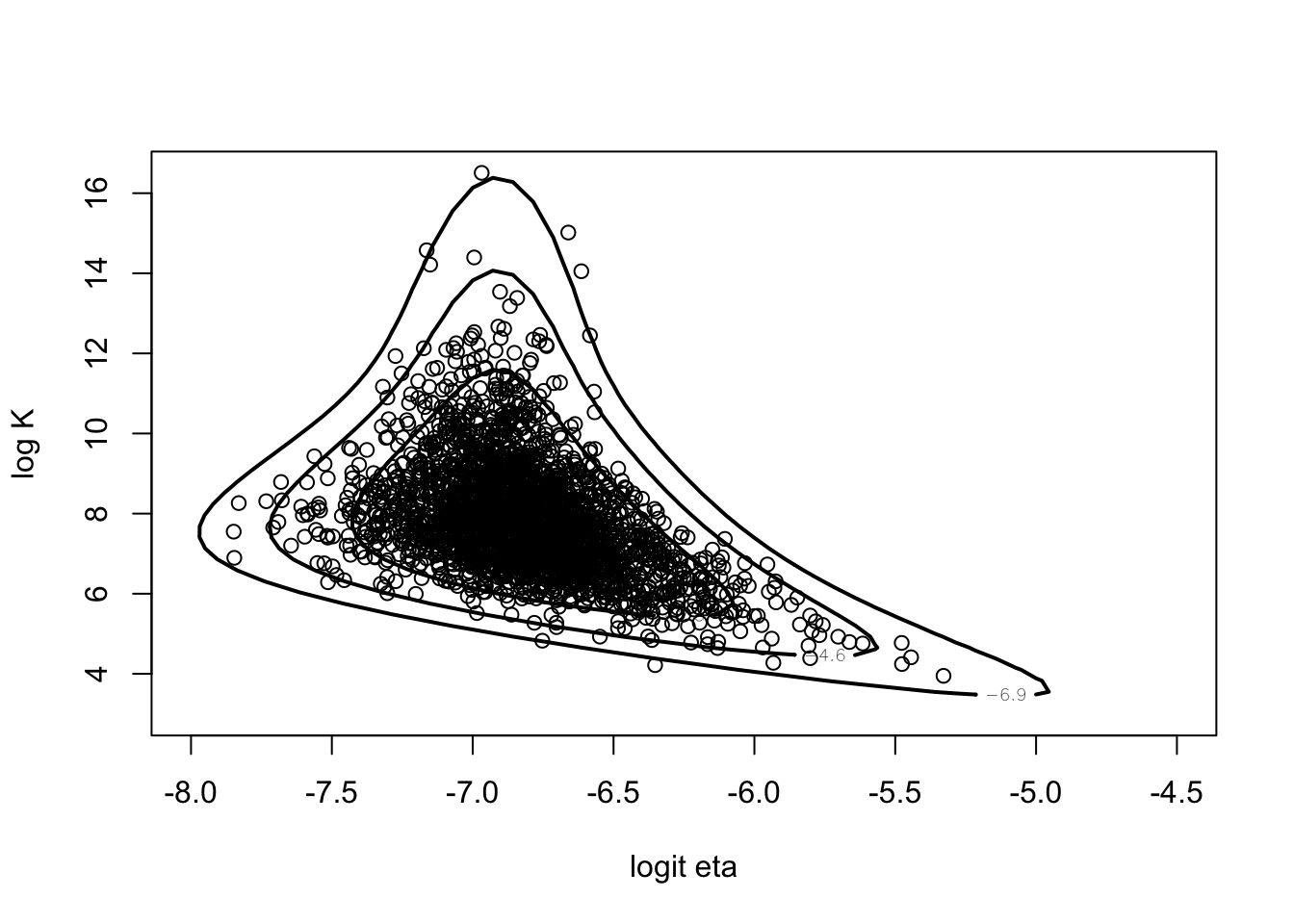

5.5 Importance Sampling

fit <- laplace(betabinexch,
               c(-7, 6),
               cancermortality)

Posterior density of \(\log K\)$ conditional on a value of \(\eta\).

betabinexch.cond <- function (log.K, data){
  eta <- exp(-6.818793) / (1 + exp(-6.818793))
  K <- exp(log.K)
  y <- data[, 1]
  n <- data[, 2]
  N <- length(y)
  logf <- 0 * log.K
  for (j in 1:length(y)){
     logf = logf + lbeta(K * eta + y[j], 
                 K * (1 - eta) + n[j] - y[j]) -
                lbeta(K * eta, K * (1 - eta))
  }
  val <- logf + log.K - 2 * log(1 + K)
  exp(val-max(val))
}

Illustrate different choices of importance sampler.

I <- integrate(betabinexch.cond, 2, 16,
               cancermortality)
par(mfrow=c(2, 2))
curve(betabinexch.cond(x, 
            cancermortality) / I$value, 
            from=3, to=16,
            ylab="Density", xlab="log K", lwd=3,              main="Densities")
curve(dnorm(x, 8, 2), add=TRUE)
legend("topright",
       legend=c("Exact", "Normal"),
       lwd=c(3, 1))
curve(betabinexch.cond(x,
            cancermortality) / I$value /
           dnorm(x, 8, 2), from=3, to=16,                 ylab="Weight", xlab="log K",
       main="Weight = g/p")
curve(betabinexch.cond(x, 
            cancermortality) /I$value, 
          from=3, to=16,
          ylab="Density", xlab="log K", 
          lwd=3, main="Densities")
curve(1 / 2 * dt(x - 8, df=2), add=TRUE)
legend("topright", legend=c("Exact", "T(2)"), lwd=c(3, 1))
curve(betabinexch.cond(x, 
          cancermortality) / I$value /
        (1 / 2 * dt(x - 8, df=2)), 
        from=3, to=16, 
        ylab="Weight", xlab="log K",
        main="Weight = g/p")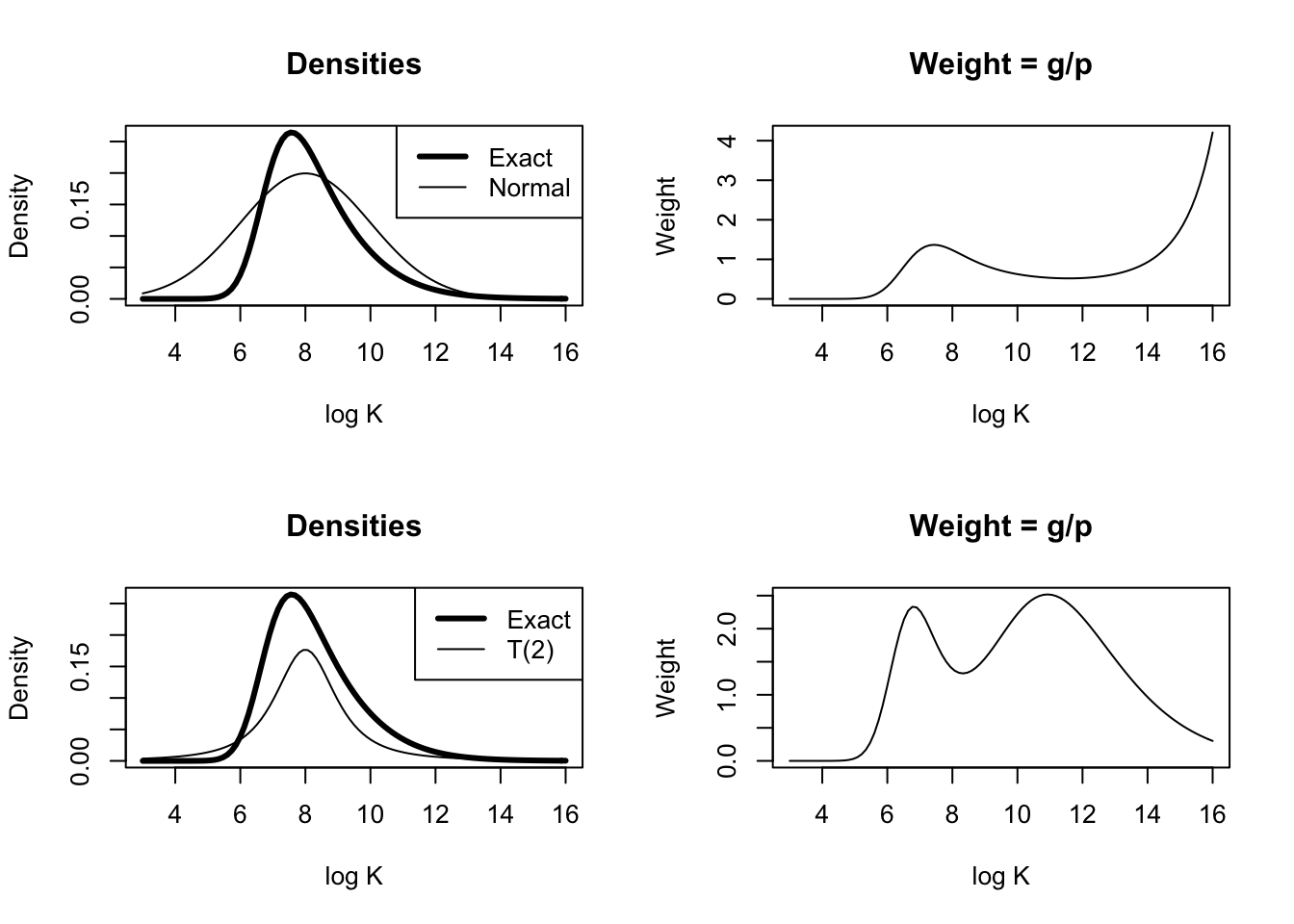

tpar <- list(m=fit$mode,
             var=2 * fit$var, 
             df=4)
myfunc <- function(theta){
   return(theta[2])
}
s <- impsampling(betabinexch,
                 tpar,
                 myfunc,
                 10000,
                 cancermortality)
cbind(s$est, s$se)

##          [,1]       [,2]
## [1,] 7.926348 0.01891307

5.6 Sampling Importance Resampling

Illustrate using the SIR algorithm for the beta-binomial density with a multivariate t proposal density.

fit <- laplace(betabinexch, 
               c(-7, 6), 
               cancermortality)

tpar <- list(m=fit$mode,
             var=2 * fit$var, df=4)

theta.s <- sir(betabinexch, 
               tpar, 10000, 
               cancermortality)

Use SIR to examine the sensitivity of the posterior inference to removal of individual observations.

S <- bayes.influence(theta.s, cancermortality)
plot(c(0, 0, 0), S$summary, 
     type="b", lwd=3, xlim=c(-1, 21),
     ylim=c(5, 11), 
     xlab="Observation removed",  ylab="log K")
for (i in 1:20){
  lines(c(i, i, i), S$summary.obs[i, ], type="b")
}