Chapter 1 Introduction to the brms Package

In Probability and Bayesian Modeling, the JAGS software is illustrated to fit various Bayesian models by Markov Chain Monte Carlo (MCMC) methods. JAGS consists of a mix of conjugate, Gibbs sampling, and Metropolis algorithms. In recent years, Hamiltonian sampling and the associated Stan software are becoming popular in fitting Bayesian models by MCMC.

The purpose of this supplement is to illustrate Bayesian fitting of common statistical models using the brms package which is a popular interface for the Stan software. This material should help the user learn the basic features of fitting Bayesian models using Stan after becoming familiar with the models in Probability and Bayesian Modeling.

1.1 Installing the brms package

Basic information about installing the brms package is available at https://github.com/paul-buerkner/brms

Since the package is an interface to the Stan software, a C++ compiler is required.

1.2 One Bayesian fitting function brm()

One attractive feature of the brms package is that one function brm() can be used to fit all of the models described in Probability and Bayesian Modeling.

The basic function syntax of the brm() function is:

brm(model_description, 
    data = my_data, 
    family = the_family,
    prior = the_prior)

where

  • model_description is the description of the regression model including any random effects similar to the notation used in the glm() and glmer functions
  • my_data is the data frame containing the data
  • family is the sampling family (normal, binomial, Poisson, etc)
  • prior is the specification of the prior on the regression terms and the error standard deviation

The output of the brm() function is an object of class brmsfit that contains the posterior samples and other information about the model.

1.3 A Nonlinear Regression Example

Here is an illustration of the use of the brms package for a nonlinear regression model applied to a baseball model.

1.4 Load in some packages.

library(Lahman)
library(tidyverse)
library(brms)
library(CalledStrike)

1.5 Data

Collect the number of wins, losses, runs scored, and runs allowed for the 30 baseball teams in the 2019 season.

Teams %>% 
  filter(yearID == 2019) %>% 
  select(teamID, W, L, R, RA) %>% 
  mutate(WL = W / L, RR = R / RA) -> d
d
##    teamID   W   L   R  RA        WL        RR
## 1     ARI  85  77 813 743 1.1038961 1.0942127
## 2     ATL  97  65 855 743 1.4923077 1.1507402
## 3     BAL  54 108 729 981 0.5000000 0.7431193
## 4     BOS  84  78 901 828 1.0769231 1.0881643
## 5     CHA  72  89 708 832 0.8089888 0.8509615
## 6     CHN  84  78 814 717 1.0769231 1.1352859
## 7     CIN  75  87 701 711 0.8620690 0.9859353
## 8     CLE  93  69 769 657 1.3478261 1.1704718
## 9     COL  71  91 835 958 0.7802198 0.8716075
## 10    DET  47 114 582 915 0.4122807 0.6360656
## 11    HOU 107  55 920 640 1.9454545 1.4375000
## 12    KCA  59 103 691 869 0.5728155 0.7951669
## 13    LAA  72  90 769 868 0.8000000 0.8859447
## 14    LAN 106  56 886 613 1.8928571 1.4453507
## 15    MIA  57 105 615 808 0.5428571 0.7611386
## 16    MIL  89  73 769 766 1.2191781 1.0039164
## 17    MIN 101  61 939 754 1.6557377 1.2453581
## 18    NYA 103  59 943 739 1.7457627 1.2760487
## 19    NYN  86  76 791 737 1.1315789 1.0732700
## 20    OAK  97  65 845 680 1.4923077 1.2426471
## 21    PHI  81  81 774 794 1.0000000 0.9748111
## 22    PIT  69  93 758 911 0.7419355 0.8320527
## 23    SDN  70  92 682 789 0.7608696 0.8643853
## 24    SEA  68  94 758 893 0.7234043 0.8488242
## 25    SFN  77  85 678 773 0.9058824 0.8771022
## 26    SLN  91  71 764 662 1.2816901 1.1540785
## 27    TBA  96  66 769 656 1.4545455 1.1722561
## 28    TEX  78  84 810 878 0.9285714 0.9225513
## 29    TOR  67  95 726 828 0.7052632 0.8768116
## 30    WAS  93  69 873 724 1.3478261 1.2058011

1.6 The Model

We consider a statistical version of the well-known Pythagorean relationship developed by Bill James. We assume that the ratio of wins to losses \(W/L\) is normal with mean given by the kth power of the ratio of runs to runs allowed \((R / RA)^k\) and standard deviation \(\sigma\).

\[ \frac{W}{L} \sim N(\left(\frac{R}{RA}\right)^k, \sigma) \] The unknown parameters are \(k\) and \(\sigma\). For a prior we assume \(k\) and \(\sigma\) are independent where \(k\) is assumed normal with mean 2 and standard deviation 0.5, and \(\sigma\) is exponential with rate 10 (mean 1/ 10 = 0.1).

1.7 Setting up the prior in the brms package

We use the prior() function to define the priors in the Bayesian fitting.

prior1 <- c(prior(normal(2, 0.5), nlpar = "b1"),
            prior(exponential(10), class = "sigma"))

1.8 Bayesian fitting

We use the brm() function to do the fitting. Note that we use the bf() argument to specify this nonlinear model. We indicate the data is in the data frame d, the prior specification is in prior1 and the family = gaussian argument indicates we are assuming normal errors.

fit1 <- brm(bf(WL ~ 0 + RR ^ b1, b1 ~ 1, nl = TRUE),
            data = d, prior = prior1,
            family = gaussian, 
            refresh = 0)
## Compiling Stan program...
## Start sampling

To confirm that we have inputted the priors correctly, we use the prior_summary() function.

prior_summary(fit1)
##             prior class      coef group resp dpar nlpar bound
## 1  normal(2, 0.5)     b                              b1      
## 2                     b Intercept                    b1      
## 3 exponential(10) sigma

The plot() function will display trace plots and density plots for each parameter.

plot(fit1)

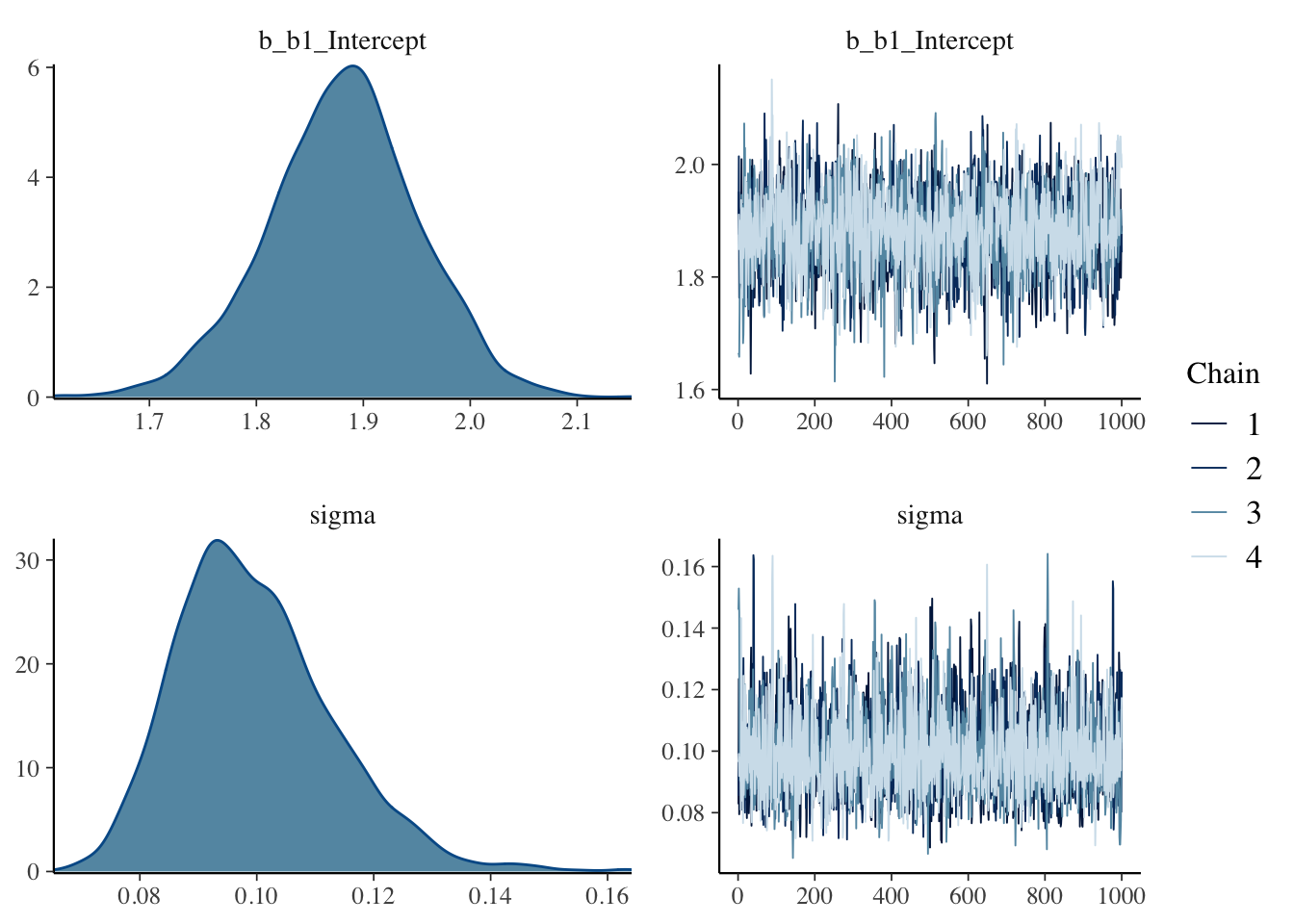
The summary() function provides summary measures for each parameter.

summary(fit1)
##  Family: gaussian 
##   Links: mu = identity; sigma = identity 
## Formula: WL ~ 0 + RR^b1 
##          b1 ~ 1
##    Data: d (Number of observations: 30) 
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup samples = 4000
## 
## Population-Level Effects: 
##              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## b1_Intercept     1.88      0.07     1.74     2.01 1.00     2967     2168
## 
## Family Specific Parameters: 
##       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma     0.10      0.01     0.08     0.13 1.00     3095     2664
## 
## Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).

The posterior_samples() function outputs a data frame of simulated draws. We show the joint posterior of \((k, \sigma)\) by displaying a scatterplot of these simulations.

par_sim <- posterior_samples(fit1)
ggplot(par_sim,
       aes(b_b1_Intercept, sigma)) +
  geom_point(alpha = 0.2) +
  increasefont() +
  ggtitle("Posterior Distribution of (k, sigma)") +
  centertitle()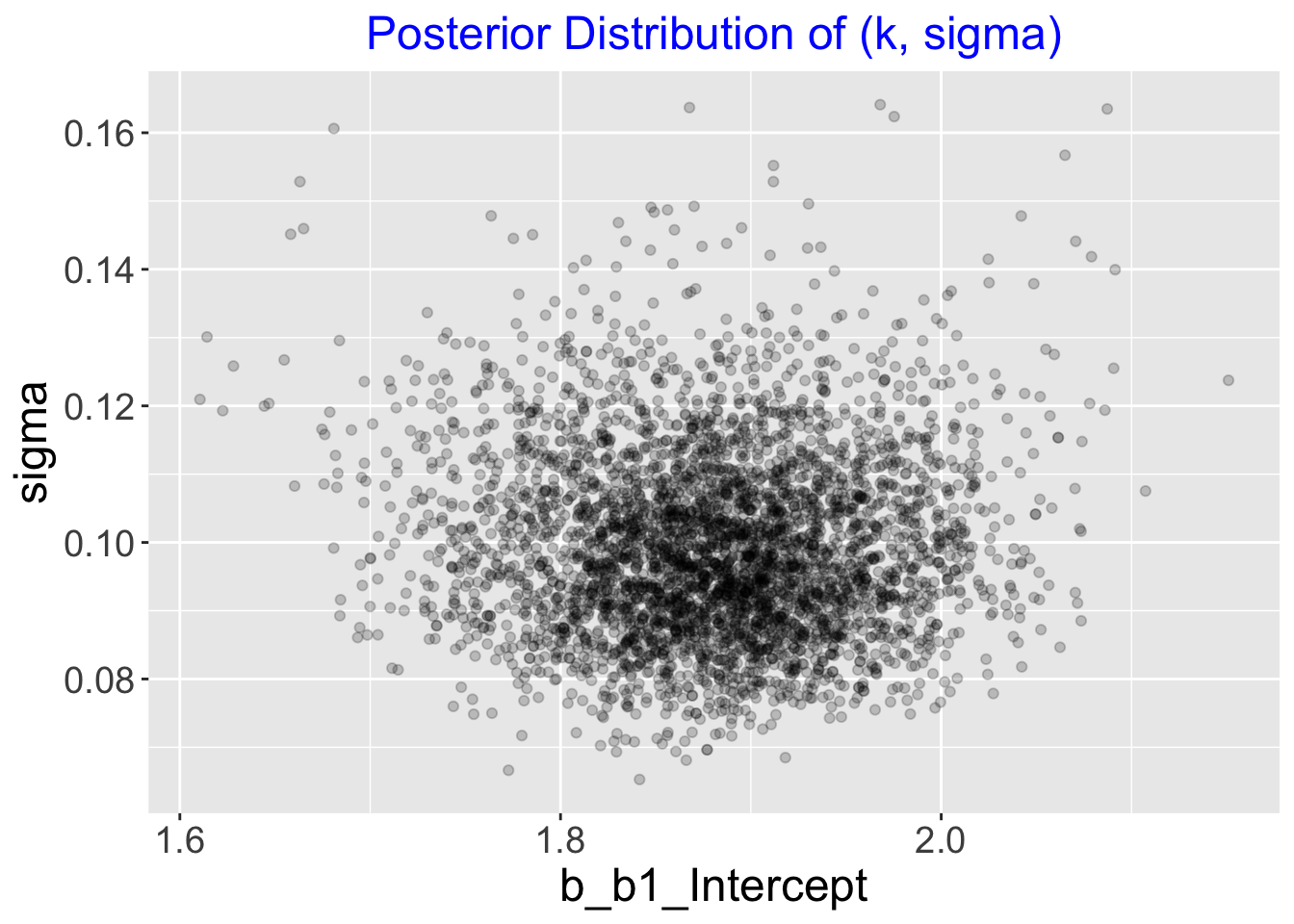

1.9 Prediction

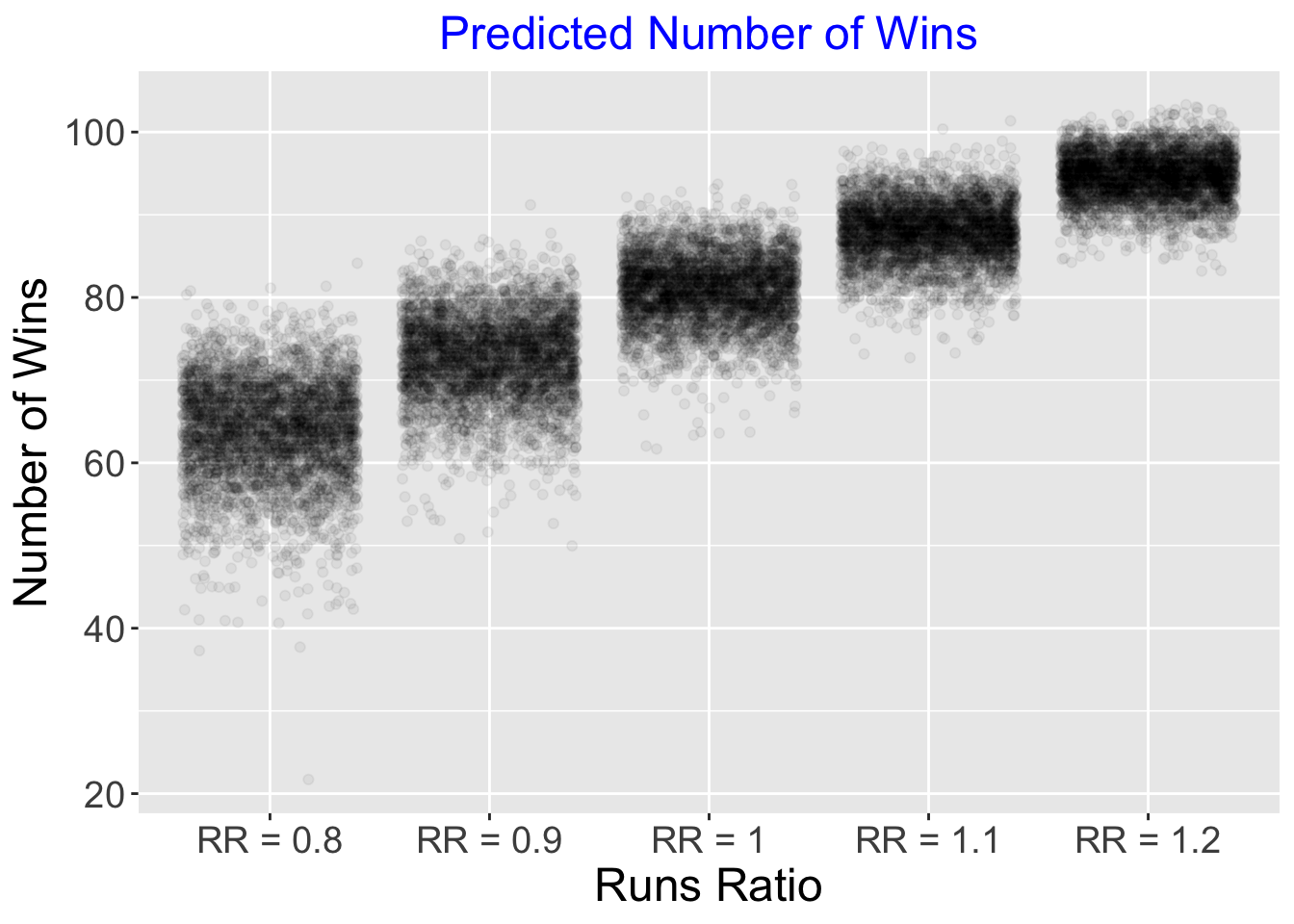
Suppose we are interested in predicting the number of games won in a 162 season given a value of the runs ratio.

We focus on runs ratio values equal to 0.8, 0.9, 1, 1.1 and 1.2. The posterior_predict() function will simulate draws of the W/L ratio from the posterior predictive distribution.

By use of the formula \[ W = round(162 \frac{W/L}{1 + W/L}) \] we convert these W/L ratios to games won in a 162 game season.

PP <- posterior_predict(fit1,
               newdata = data.frame(
                RR = seq(0.8, 1.2, by = 0.1))) 
P_Wins <- round(162 * PP / (PP + 1)) %>% 
  as.data.frame()
names(P_Wins) <- paste("RR =", 
                       seq(0.8, 1.2, by = 0.1))

I construct jitter point clouds for the number of wins for teams with each value of the runs ratio.

P_Wins %>% 
  pivot_longer(
    cols = starts_with("RR"),
    values_to = "Number_of_Wins"
  ) -> P_Wins2
ggplot(P_Wins2, aes(name, Number_of_Wins)) +
  geom_jitter(alpha = 0.05) +
  increasefont() + 
  xlab("Runs Ratio") +
  ylab("Number of Wins") +
  ggtitle("Predicted Number of Wins") +
  centertitle()