5 Boxplots
5.1 The Data:
In this topic, we start discussing how to compare batches of data effectively. Our dataset is taken from the 2001 Boston Marathon race. On the www.bostonmarathon.org website, one can obtain results for participants of different genders, ages, and home countries. Here we focus on the time-to-completion for woman runners. We take a sample of women of ages 20, 30, 40, 50, and 60. In the display below, we show the data and then construct parallel stemplots of the times (in minutes) for all the runners in our study. The unit in our stemplot is one, so the shortest time among all 20-year women in our sample had a finish time of 150 minutes, which is equivalent to 2 1/2 hours.
Official times (minutes) of some women runners in the 2001 Boston Marathon.
Age=20
244 213 274 240 225 269 214 223 271 237
232 229 209 272 230 229 203 236 222 239
233 150
age=30
194 207 259 287 319 252 237 330 236 210
226 213 241 235 194 216 272 227 278 211
219 259 237 234 205
age=40
286 256 247 166 275 284 239 235 163 214
227 346 210 223 238 221 271 224 248 231
314 224 258 244 262
age=50
281 287 222 251 253 302 235 231 254 253
262 231 230 284 326 349 269 327 258 270
260 279 263 245 271
age=60
219 338 278 315 278 258 274 233 280 270
271
PARALLEL STEMPLOTS
One unit = 1 minute.
AGE=20 AGE=30 AGE=40 AGE=50 AGE=60
15 0 15 15 15 15
16 16 16 36 16 16
17 17 17 17 17
18 18 18 18 18
19 19 44 19 19 19
20 39 20 57 20 20 20
21 34 21 01369 21 04 21 21 9
22 23599 22 67 22 13447 22 2 22
23 023679 23 45677 23 1589 23 0115 23 3
24 04 24 1 24 478 24 5 24
25 25 299 25 68 25 13348 25 8
26 9 26 26 2 26 0239 26
27 124 27 28 27 15 27 019 27 01488
28 28 7 28 46 28 147 28 0
29 29 29 29 29
30 30 30 30 2 30
31 31 9 31 4 31 31 5
32 32 32 32 67 32
33 33 0 33 33 33 8
34 34 6 34 34 9 34We are interested in graphically comparing the batches of times from the five age groups. An effective display is based on a boxplot, which is a graph of a five-number summary with outliers indicated.
5.2 Constructing A Single Boxplot
Let’s first illustrate the construction of a single boxplot for the times of the 20-year old women. There are \(n\) = 22 runners. So the location of the median is (22+1)/2 = 11 1/2, and the location of the fourths is (11+1)/2 = 6. From the stemplot, we find
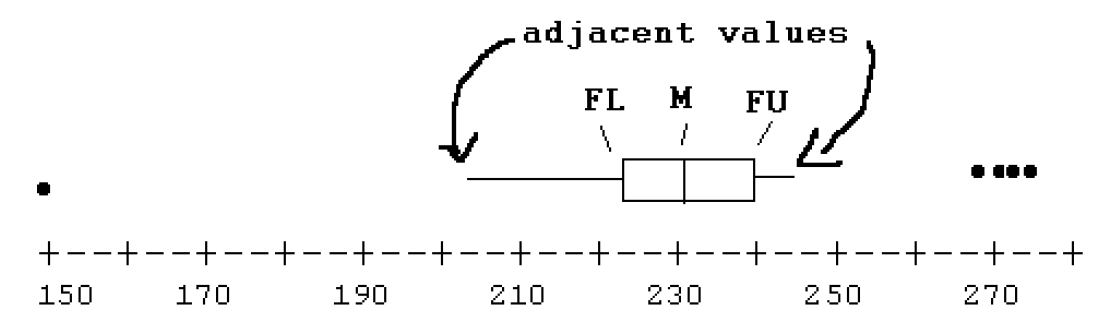
\[ LO = 150, F_L = 222, M = 231, F_U = 240, HI = 274 . \]
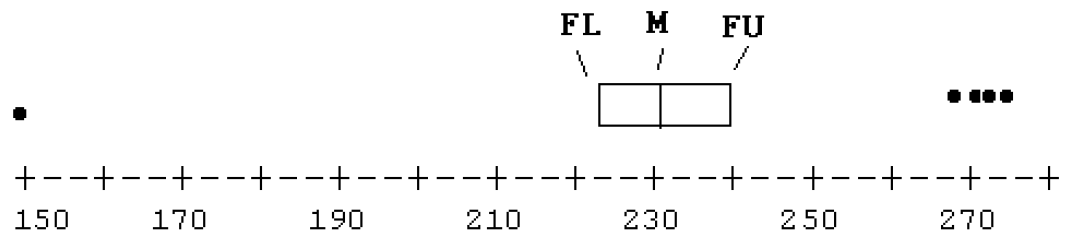
Do we have any outliers? Here the fourth spread is \(d_F = 240 - 222 = 18\) and a step is 1.5 (18) = 27. The inner fences are at \[ 222 - 27 = 195 \,\, {\rm and} \,\, 240 + 27 = 267 \] Looking at the stemplot, we see one time (150) beyond the lower fence and four times (269, 271, 272, 274) beyond the upper fence. Certainly the low outlier is interesting since that corresponds to a very fast marathon runner.
To draw a boxplot:
- Draw a number line with tic marks covering the range of the data.
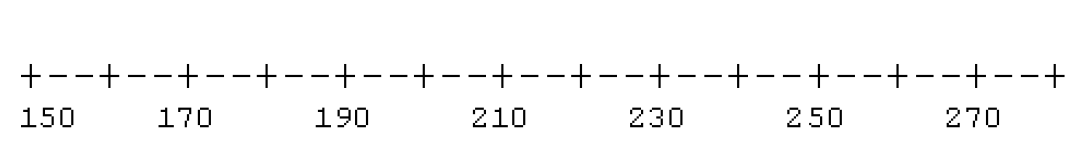
- Draw a box where the lines of the box correspond to the locations of the fourths and the median. (See diagram.)
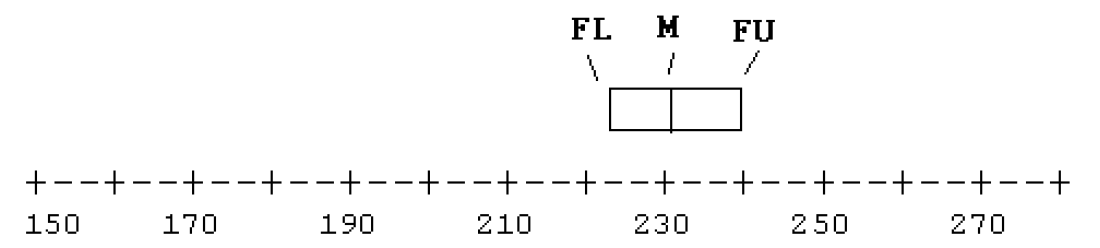
- Indicate the outliers using separate plotting points.
- To complete the box, draw lines out from the box to the most extreme values that are not outliers. (These points are called adjacent values.)
Of course, we don’t need our labels and so our boxplot would look like

Here is a software generated boxplot display using the ggplot2 package in R.
library(LearnEDAfunctions)
library(tidyverse)
ggplot(filter(boston.marathon, age == 20),
aes(x = 1, y = time)) + xlim(0, 2) +
geom_boxplot() + coord_flip() +
theme(axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank())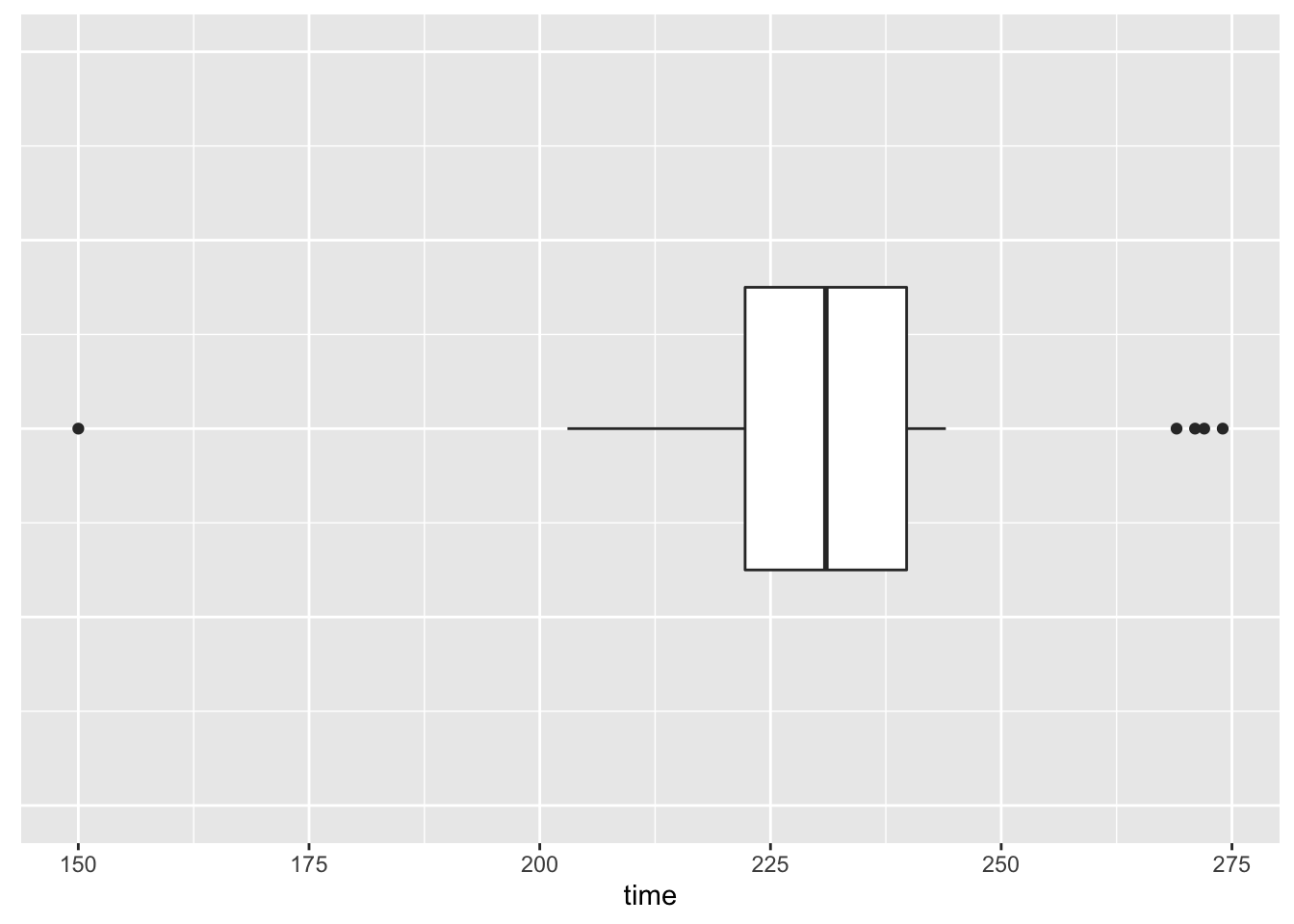
5.3 Interpreting a Boxplot
Before we use boxplots to compare batches, let us spend some time interpreting a boxplot for a single batch. The figure below shows the histogram and corresponding boxplot for two datasets. The first dataset (left side) is symmetric with long tails on both sides.
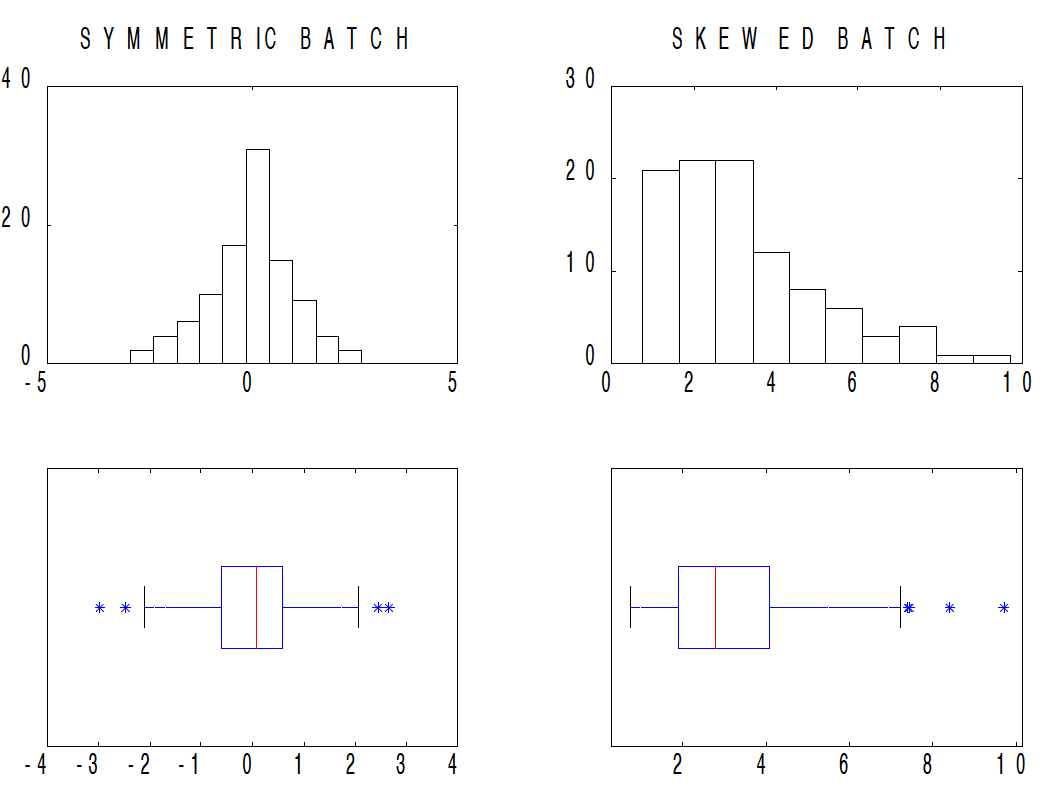
If we look at the corresponding boxplot of this symmetric dataset, we see
- the location of the median (red line) is roughly half-way across the box (the location of the fourths)
- the lengths of the right and left whiskers (the lines extending from the box) are about the same – this means that the width of the lower quarter of the data is equal to the width of the upper quarter
Let’s contrast this boxplot of the symmetric batch with the boxplot of the batch on the right. From the histogram, we see that this data is skewed right – most of the data is in the 0-4 range and the values tail off towards large values. If we look at the corresponding boxplot, we see
- the length of the box from the median to the upper fourth is longer than the length from the lower fourth to the median – this indicates skewness in the middle half of the data
- the length of the right whisker is significantly longer than the length of the left whisker – this shows right skewness in the tail portion of the data
After some practice looking at boxplots, you’ll see that a boxplot is pretty informative about the shape of a batch.
5.4 Boxplots to Compare Batches
Now we are ready to use boxplots to compare the batches of running times for the different age groups. For each batch, we compute (1) the five-number summary, (2) the fences, and (3) indicate any outliers. Below, we have summarized our calculations for the five age groups, and then we use the calculations to construct boxplots for the batches. We display all of the boxplots on a single plot using one scale.
Age = 20
Depth Lower Upper
N= 22
M 11.5 231.000
F 6.0 222.000 240.000
STEP = 27
FENCES = 195, 258
OUTLIERS: 150, 269, 271, 272, 274
Age = 30
Depth Lower Upper
N= 25
M 13.0 235.000
F 7.0 213.000 259.000
STEP = 69
FENCES: 144, 328
OUTLIERS: 330, 346
Age = 40
Depth Lower Upper
N= 25
M 13.0 239.000
F 7.0 224.000 262.000
STEP = 57
FENCES = 167, 319
OUTLIERS: 163, 166
Age = 50
Depth Lower Upper
N= 25
M 13.0 262.000
H 7.0 251.000 281.000
STEP = 45
FENCES: 206, 326
OUTLIERS: 327, 349
Age = 60
Depth Lower Upper
N= 11
M 6.0 274.000
H 3.5 264.000 279.000
STEP = 22.5
FENCES: 241.5, 301.5
OUTLIERS: 219, 233, 315, 338ggplot(boston.marathon, aes(x = factor(age), y = time)) +
geom_boxplot() + coord_flip() +
xlab("Age") + ylab("Time")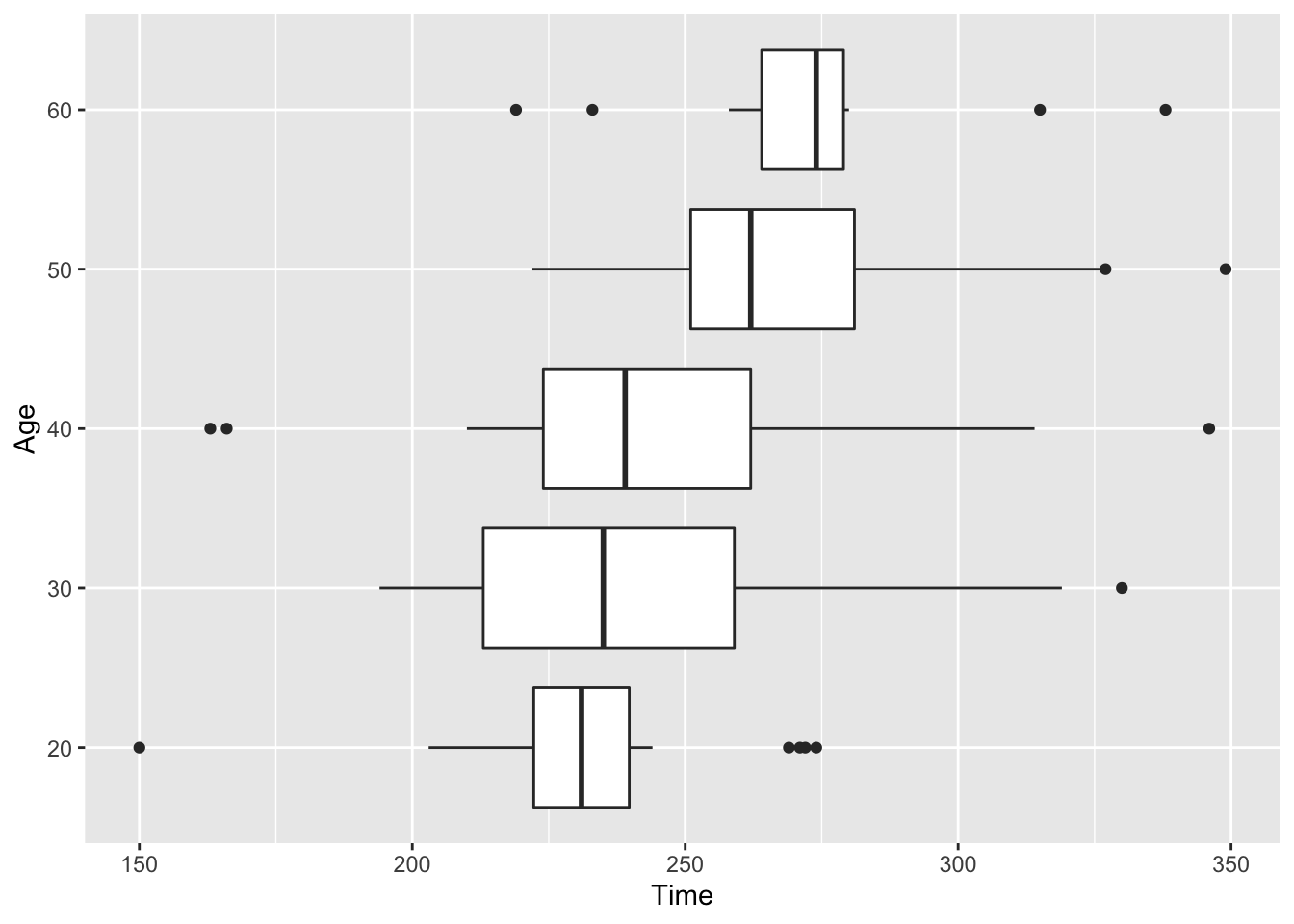
What do we see in this display of boxplots?
It is easier to interpret this display when the boxplots are sorted by the medians of the groups. Here this sorting occurs naturally, since the 20 year-olds generally have smaller times than the 30 year-olds, and the 30 year-olds have smaller times for the 40 year-olds, and so on.
We notice a number of outlying points. In each age group, there are one or two unusually large times. Since we give special recognition to short times, we notice the 20-year woman who ran the race in 150 minutes.
If we focus on the three middle age groups, we notice that each group has about the same spread. (The spreads of the times for the 20 year-olds and the 60 year-olds are a bit smaller.) The lengths of the boxes for the three groups are about the same, indicating they have similar fourth spreads.
5.5 Comparisons using Medians
When batches have similar spreads, it is easy to make comparisons. Let’s illustrate this for the three middle age groups that have similar spreads. The medians and fourth spreads for these batches are
Median Fourth-Spread
age30 235 min 46 min
age40 239 min 38 min
age50 262 min 30 minSince the times for the 30-year-old and 40-year-old groups have approximately the same spread, the batch of 40-year-old times can be obtained by adding 4 minutes (the difference in medians) to the batch of 30-year-old times. In other words,
\[ age40 = age30 + 4 \] which means that the 40-year-olds run, on average, 4 minutes longer than the 30-year-older runners.
Similarly, comparing the two older groups, we can say that \[ age50 = age40 + 23 \] which means that the batch of 50-year-old times can be found by adding 23 minutes to the 40-year-old times.
Do older women runners run slower than younger women in the Boston Marathon? Looking back at our boxplot display and comparing medians of the five groups, we see that women of ages 20, 30, and 40 have (approximately) the same median completion time. The median time for the 50 year-old runners seems significantly higher that the times for the 20-40 year-olds, and the runners of age 60 have a significantly higher median than the 50-year-olds. So it appears that the best times for women marathoners are in a broad range between 20 and 40 years, and the times don’t appear to deteriorate until after age 40.
This is a nice illustration, since the batches of data had similar spreads and this facilitated comparisons by comparing medians. We will see in our next example that batches can have varying spreads and this motivates a reexpression or change in the scale of the data so that the reexpressed batches have similar spreads